Got It is an adding game for two players. You can play against the computer or with a friend.
The task is below, or you can download it here as a Word document.
Rules:
The first player chooses a whole number from 1 to 4.
Players take turns to add a whole number from 1 to 4 to the running total.
The player who hits the target of 23 wins the game.
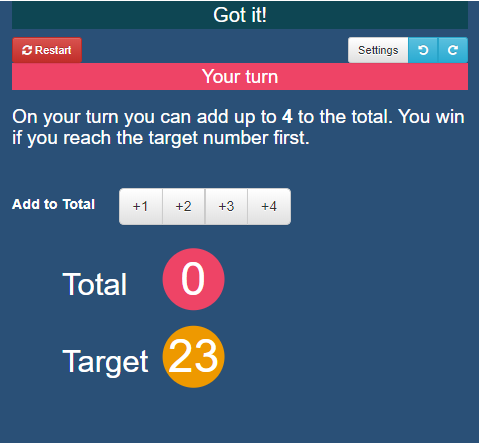
Task 1
Here is a scoresheet from my game against the computer.

Can you work out the missing numbers?
Who won the game?
Play the game a few times against someone at home or over the phone, or play against the computer here: https://nrich.maths.org/gotit/. Record each game in a table like the one above.
Task 2
The main goal of this activity is to try and find a winning strategy.
- You might already have an inkling of what a winning position looks like – if so, write it down now.
Alternatively, you might have spotted that there was some position that was impossible to win from. This is especially likely to be the case if you played against the computer, which always plays the best possible move. However, it CAN be beaten.
- Look at the tables you made in the first task. Highlight any totals that appear in every table where you won, and highlight any totals that appear in every table where you lost.
- Are there any totals that seem to always lead to you winning or losing?
Task 3
Here are some screenshots from games against the computer.
- Which of these positions can you definitely win from?
- Which will the computer definitely win from?
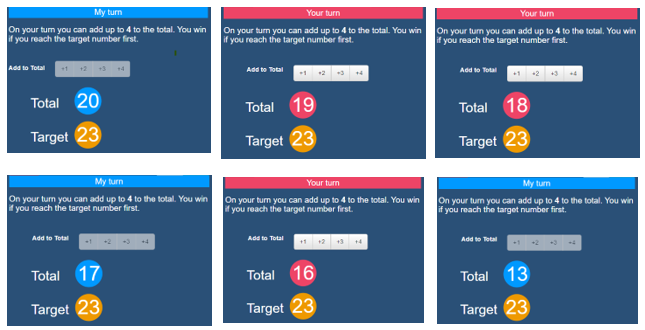
- What stepping stones should you try to hit on your way to 23 if you want to win?
Play the game a few more times.Can you come up with a winning strategy?
- Describe a strategy that will always beat the computer.
Task 4
You can play this game with other totals, and with other possibilities for each move.
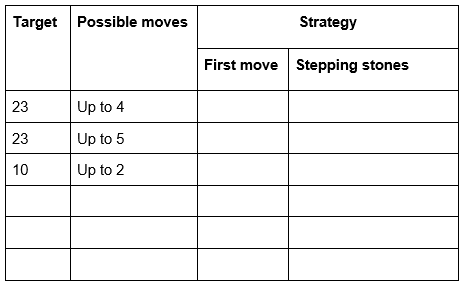
- What would a winning strategy look like if the total was 23 but you could choose numbers up to 5 instead? Try it out against the computer here: https://nrich.maths.org/gotit/#/number/23/5/1/0
- What would a winning strategy look like if the total was 10 and you could only choose 1 or 2 each time? Try it out against the computer here: https://nrich.maths.org/gotit/#/number/10/2/1/0
If you’re playing against the computer, you can change the game for yourself by clicking on Settings.
- Try some different set ups, and record your results in a table like this.
The challenge
- Can you come up with a general rule for the best strategy, so no matter what the target and possible moves are, you always win?
- Find an opponent at home. Tell them to choose their own target, and their own possible moves. Then use your strategy to beat them!
- It’s possible your opponent will think it’s unfair if you always go first. Can you adapt your strategy to allow them to start?