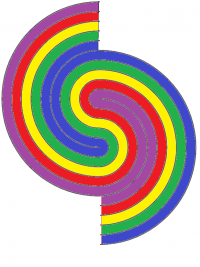By Mark Dawes and Cate Middleton (September 2019)
Mark writes:
Cate Middleton, subject leader for mathematics at Littleport and East Cambs Academy is keen on mathsy art. When I saw some of the things she has done with her pupils I was blown away by both the quality and the quantity of the ideas she had gathered from lots of different places. With Cate’s permission, I share some of these here.
One of the things I loved about seeing this work was that I could interact with it in a creative way too. It also made me think.
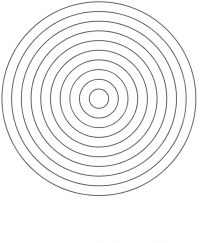
For example, Cate started with some concentric circles.
Cate’s pupils made bookmarks (which were later laminated for them to keep and use), they moved half of the image downwards and they played with quarters of the image:
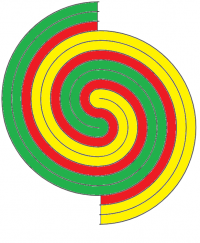
I found this fascinating! I was interested in what happened if I moved half the image down by different amounts. How many separate sections would I get?
Rather pleasingly, if you move it down one line you get a continuous spiral, which only needs one colour. Moving it down two lines gives you two separate sections. Moving three lines give you three sections … etc. I wasn’t expecting that.
If we cut the original concentric circles into quarters there are 44 = 256 different ways to put them together (although many of those will be rotations and reflections of other possibilities). Here are a few of my favourites:
Anamorphic art
I love anamorphic art. I am fascinated by the adverts you see painted on sports pitches, for example, and much prefer to see them from an angle other than the one intended by their creators:
[NRICH has an article on this: https://nrich.maths.org/7023 ]
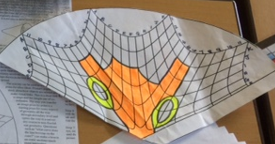
I hadn’t ever seen it on a cone. Templates are available here:
https://anamorphicart.wordpress.com/2010/04/21/cone-grids-and-images-to-download/
if you wrap it round to make a cone, when you look vertically downwards onto the cone you see the image as intended. For example, this one, when assembled, makes a car:
Tetrahedra
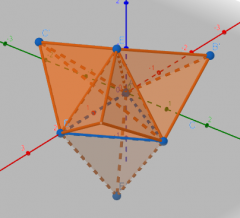
I find 3D imagery hard! I tried to imagine what would happen if I made 5 tetrahedra and stuck four of them onto the four faces of the other tetrahedron. GeoGebra 3D helped me to see what was going on.
Cate had a far nicer idea with these. A Sierpinski Tetrahedron!
Here’s are some stage 2 Sierpinski Tetrahedra.
And here’s a stage 3 one:
I like the idea that pupils could construct their own nets for these, that all of them could be involved in making tetrahedra and that the final version therefore becomes a piece of art created by the whole class.
Hexaflexagons
These look great, are surprising and interesting. And they move!
Templates are here: http://www.auntannie.com/Geometric/Flexagon/
Hexagon-based tessellations
Start with a regular hexagon (which self-tessellates). Make changes to it. Does it still tessellate? This is beautiful (and very clever!). I wonder whether Escher did it like this?
Mondrian Maths:
Here are some beautiful pictures that are clearly inspired by Mondrian.
But why just make them flat? Here are more in 3D!
How many do we need to make a work of art?
Final thoughts:
These are within my capabilities – and give how hard I have to work to make art that looks anything like it should, that probably means the vast majority of pupils can attempt these too.
Thanks to Cate for compiling such a wide selection of materials and ideas.