by Mark Dawes, Nov 2018
Pupils who do not have English as their first language face a number of challenges when learning mathematics and may need support in different ways.
There seem to me to be several issues for pupils with English as an Additional Language (EAL):
- Use of mathematics-specific vocabulary
- Use of ordinary English
- Other mathematical norms
- Use of mathematics in their first language.
- Individual differences
I will expand on each of these in turn.
1. Use of mathematics-specific vocabulary
One of the first things teachers sensibly try to do to support pupils with EAL is to simplify the language they use. This should only be the case for the ‘ordinary’ English that is used. The mathematics-specific vocabulary that we use is important and all pupils need to hear it and to be able to use it correctly. We cannot, therefore, always simplify mathematical words, so pupils need to hear and use ‘subtract’, ‘take away’, ‘minus’, ‘difference’, etc, partly because they have slightly different meanings and there are nuances that might otherwise be lost.
In many ways it is easy to support children with EAL in using maths-specific vocabulary. We can give the pupils lists of terms and key mathematical words for the topic. We can ask teachers or teaching assistants in school who speak that language for help with translations. We can ask for parental assistance and can also use ICT to help. While it is appropriate to be wary of Google Translate (which sometimes fails to pick up the intended meaning of words with many uses; just think of the different things that the word ‘pound’ can mean: money, weight, to hit, a place to take lost dogs), WordReference.com is often very good because it gives example sentences and provides context.
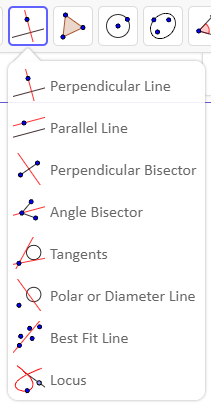
The GeoGebra software includes lots of mathematical vocabulary in its menus and these menus have been translated into many different languages. Pupils could compare the words in the English version and in their own language (more on how to do this is below).
2. Use of ordinary English
This is perhaps harder to do. We are used to all pupils finding mathematical vocabulary difficult, but it is harder to foresee how pupils might misunderstand ordinary English and how to simplify it appropriately.
The question “what is the area of a circle radius 5cm?” is perhaps different from “What is the area of a circle?” and “what does ‘area of a circle’ mean?”. Is the answer to the first question “25pi”, the second ”pi r squared” and the third “the amount of space inside a circle”? Or are there other interpretations? And will pupils with EAL find it harder to understand the difference?
Then there is ordinary classroom language; how many instructions are given verbally in lessons, how much teaching happens verbally?
Pupils who have recently come to the UK might also face other cultural differences and have differing expectations of school. Examples include the amount of homework that is set, the way pupils and teachers treat each other and even the direction that text is written. While I was expecting the Arabic and the Hebrew settings in GeoGebra to write the text in those languages from right to left, I was surprised when the icons moved to the right-hand side and changed order. Here is a screenshot of the English toolbar:
And here is the Arabic toolbar:
Then there is the matter of handwriting vs printing. We are used to seeing the letter ‘a’ and the letter ‘g’ looking different when printed (depending on the font) from the way we handwrite them. When I handwrite the letter ‘x’ as part of a word it looks like a cross, but when I use it in algebra it looks like a reflected letter c next to a non-reflected letter c. These are all things that EAL learners will find more challenging.
3. Other mathematical norms
We often think of maths as a ‘universal language’, but there are lots of country-specific differences in the usage of mathematics and symbols. For example, in some countries a horizontal line is placed over recurring digits, whereas in England we place a dot over the first and last recurring digit. In some parts of Europe the colon symbol is used to mean division. This could be very confusing if a teacher uses the same symbol to stand for a ratio without warning the pupils that this is what it means. Not every part of the world gives the general form of a straight line as y = mx + c, with many countries using y = mx + b instead.
In some languages explanatory text is written from right-to-left and mathematics from left-to-right. If that is what you are used to, might you expect that English, which is written left-to-right, inverts its mathematics?
4. Use of mathematics in their first language.
I think we need to be aware of whether pupils are meeting a concept for the first time in English or whether they already know of the concept in their own language. This can make a big difference. If pupils know about it already they may need not only to translate the language but also how it is presented, whereas if they are meeting the concept for the first time they need to learn this (just like everyone else in the class does).
The title of this blog “a two-way process” is designed to suggest that when pupils learn some new mathematics in English they should then translate it back to their first language. Otherwise they will have a dual-language knowledge of mathematics up until a certain point and a purely English knowledge after that, whereas they should be able to function mathematically in both languages and in conversation with all members of their family.
(Stephen Fry’s Hungarian grandfather referred to what Fry heard as “Peter Gorus”; it would have been ideal for Fry to have known the different pronunciation of ‘Pythagoras’ to enable him to talk to his grandfather about it. See https://www.youtube.com/watch?v=MCLwkS9RlQ4 )
How can we encourage and support children to translate new words and concepts to their first or family language? Can we involve parents in doing this? Are some of the ICT tools mentioned earlier helpful?
5. Individual differences
Finally, we need to remember that not all pupils with EAL will respond in the same way in our mathematics classrooms. Pupils with English as their first language react differently. Some are shy, others are confident, some like to talk in class, while others are unsure of themselves, etc. This is the same for pupils with EAL too.
Pupils may be different ages when they start to be taught maths in English, will have had different prior experiences, may have had time away from formal schooling, and will perhaps have missed topics or concepts usually taught at a different time in England than in other countries. Children who were born in the UK but whose family do not all speak English at home will have different needs from those who have just arrived from abroad. Some languages are closer to English than others and this will have an effect. And then some pupils have a greater general facility with learning, take to languages more readily and have a better ‘musical ear’. We need to be able to support everyone, regardless of their differences.
GeoGebra how-to
To change the language of GeoGebra, either open the installed program on your computer or go to www.geogebra.org and select ‘GeoGebra Classic’.
From the uppermost ‘hamburger’ menu select ‘settings’ and then choose the relevant language.
When you click on one of the icons to reveal the related tools the language will have changed. Here is the same menu in English (UK) and Spanish (España):