By Mark Dawes (June 2019)
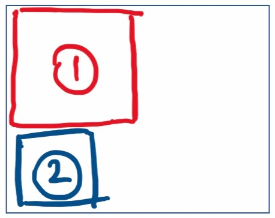
This Year 6 SATS question from the 2019 paper 2 (Adam’s rectangle) has appeared in the press and on social media and has been commented on extensively because of its perceived level of difficulty and because of the wording that is used.
I am not going to write whether pupils found it hard to understand or to answer, whether it was a reasonable question or whether it should be worth more than one mark.
Instead I want to explore a few interesting things about the question.
First I will look at the problem-solving aspects:
- What is it that makes it difficult?
- How might we support children to get started on a question like this?
Then I want to think about the scenario itself. This is not intended as a teaching tool, or as a way to answer the question, but rather to demonstrate that more, interesting things often crop up if a problem is considered more generally.
- Which other rectangles can be divided up in this way and is there a single unique way to do this?
What is it that makes it difficult?
- It’s novel. I haven’t seen a question like this before and I suspect children won’t.
- It isn’t obvious that it will always be possible to answer questions that look like this (see later in the post for more on this).
- The children are under time-pressure and in a stressful situation. No matter how well the school is supporting the pupils, there is something inherently stressful about working under exam conditions. I have just finished taking the GCSE Spanish exams, a qualification I have been doing for fun and which has no real meaning for me; I was still nervous before each exam!
- There is no rough paper to allow you to make a first attempt and then to try again.
- You need some self-confidence to get started. “I don’t know what to do” seems like a perfectly reasonable first response to this question. Having the tenacity to try something out is important.
- There is a need to bridge between a real-world scenario and a mathematical scenario. Realising that Adam is irrelevant here is the first stage. Then you need to imagine doing the cutting. After that you have to wonder whether cutting is the same as drawing lines. I wouldn’t be surprised if some people wondered whether both cuts have to go all the way across the rectangle, for example.
How might we support children to get started on a question like this?
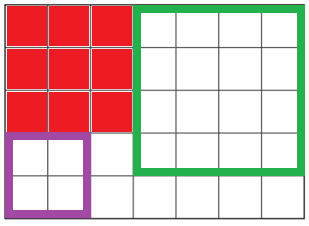
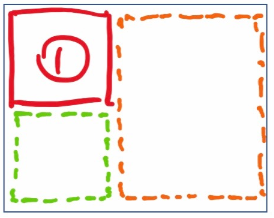
If I ask you “what’s the biggest square you can draw on the grid?” then the problem becomes easy:
Now we can see space for a square on the right-hand side, leaving a 2 by 3 rectangle below it.
Is it reasonable to ask pupils this question, though? Does that help them too much? Or is ‘trying the biggest thing that will fit’ a reasonable strategy that might also work in some other mathematical problems?
Perhaps better advice would be “try one out”. Implicitly here I am saying “let’s start with one square and see where that fits”. Then we can try to put in the second square and can see whether the space that is left is rectangular. Is discussing this as a starting point more helpful?
What if we start with a different size of square? Let’s put in a square of side 3. None of the other squares we can put in will leave us with a single rectangle. (Two possible additional squares are shown here.)
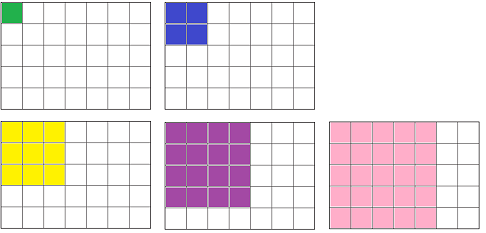
There are 85 different squares we could draw on the original grid, so drawing all of them, or drawing one ‘at random’ doesn’t seem like a good plan. So perhaps the next question to ask is “where is it sensible to put the first square?”.
If the first one is wedged in one of the corners that only leaves five possibilities.
If we are able to use squared paper and could try out drawing the second square we can see fairly quickly that some of these are not possible. It might be helpful to talk to pupils about ‘trying out an initial idea’ as a strategy.
Which other rectangles can be divided up in this way and is there a single unique way to do this?
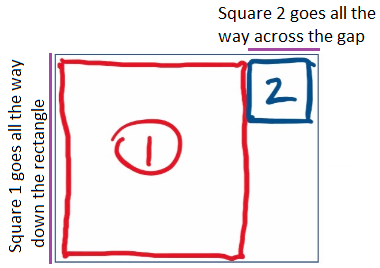
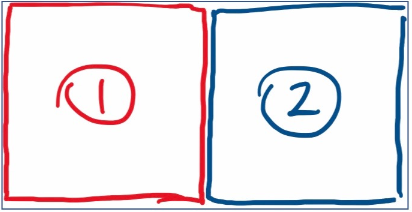
In our answer the red square went all the way down the initial rectangle. We can rotate or reflect that answer, so these are essentially all the same:
Is it possible for us to have an answer where the red square doesn’t go all the way down?
Here is an opportunity to introduce some ‘proof by contraction’. I will assume it is possible, will then arrive at a problem and will conclude that the original statement (that it’s possible) must be false.
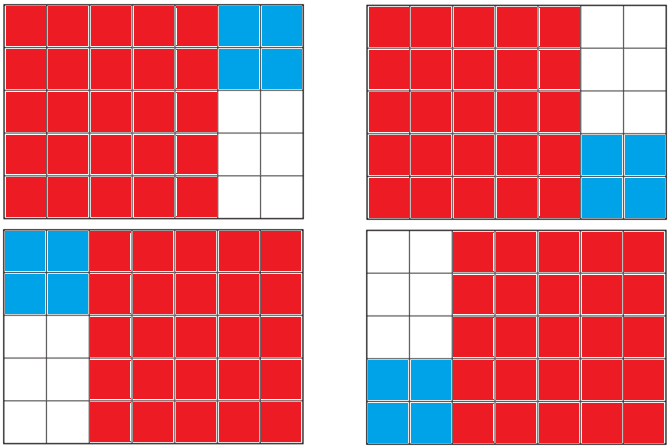
I have put the original red square in the corner of the rectangle (I am using a gridless rectangle now so I can draw a more general diagram rather than one specific case). If I now put a smaller blue square underneath it (as shown) then the remaining space isn’t a rectangle.
There are only two ways to leave a rectangle after placing the second square. Both are shown on this diagram (with one in green and the other in orange).
Hold on, though: the green one lines up with the red one, so it’s the same size – and the question says the two squares are different sizes. The orange one goes down the whole rectangle, which is what we were trying to avoid. Therefore the only way to do this is to include a big square that goes all the way down the initial rectangle.
It is possible, then, to divide up every size of rectangle into two different-sized squares and a rectangle?
From what we have done already, we need to have one square that goes all the way down the rectangle and another that goes all the way across the gap that’s left:
The first obvious problem is “what happens if the gap is a square?”.
Here we get two squares (that are the same size) and no space for a rectangle, so that doesn’t work.
If it gets any wider than this then it still doesn’t work:
There is now a space for a rectangle but the squares are the same size.
If the original rectangle is also a square then it won’t work, and if the rectangle is taller than it is wide, then it’s the same as if we rotate or reflect the landscape version.
This means if we pick a height for the initial rectangle, the width must be bigger than the height but less than double the height.
For example, if the height is 4 then the width can be 5, 6 or 7.
When the height is 4 there are three possible widths that work. How many widths are there if the height is 10? What about if the height is n ?
I mentioned earlier that you can draw 85 different squares on the original diagram from the question. How can you show that it is 85?
Final thought: on the original question the area of the rectangle is 7 x 5 = 35, and the biggest square number that fits in there is 25. Is that a useful starting point to solve this question and others like it?
.