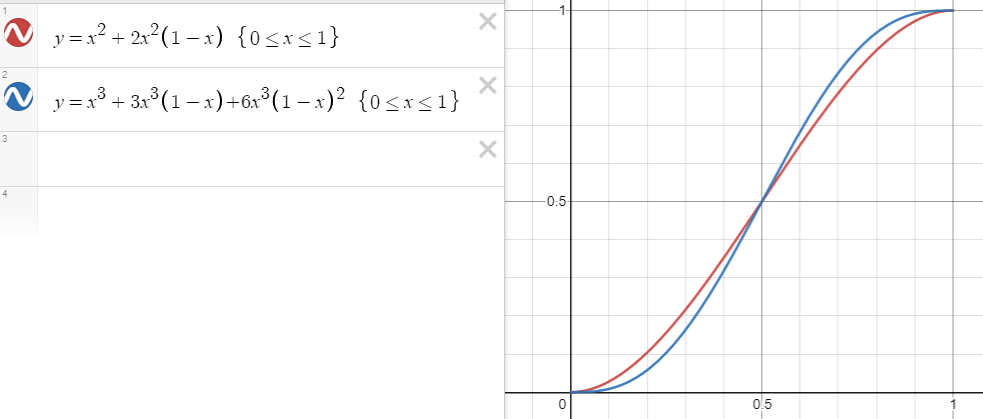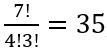by Mark Dawes (October 2021)
I thoroughly enjoyed watching tennis this year (Wimbledon, New York, etc) and have, naturally, been thinking about some of the maths behind the tournaments. In the four grand slam tennis tournaments, the women’s events are best of three sets, while the men’s events are best of five sets. What effect does this have on whether the ‘better’ player is likely to win?
I am going to recount what I did while thinking about this. There are several reasons for sharing this:
- It shows how some GCSE probability can be applied to a problem
- It shows how a problem can be tackled using maths from different levels
- It allows a discussion of probability models
- It can be extended in interesting ways
- This might be useful for A-level mathematics students to see, as an introduction to using the binomial distribution
Naïve gut-feeling
It feels reasonable that the better player is more likely to win if there are more sets. Let’s simplify this and compare a 1-set match to a 3-set match. If the weaker player happens to prevail in set 1 then they have won the 1-set match, but in the 3-set match there is still an opportunity for the stronger player to win the next two sets, and they are more likely to win them because they are the stronger player.
How could we model this?
I am going to assign a probability that the stronger player wins each set and will assume that this is independent (ie that in a particular match the probability they will win a set is the same all the time).
3-set match – a tree diagram
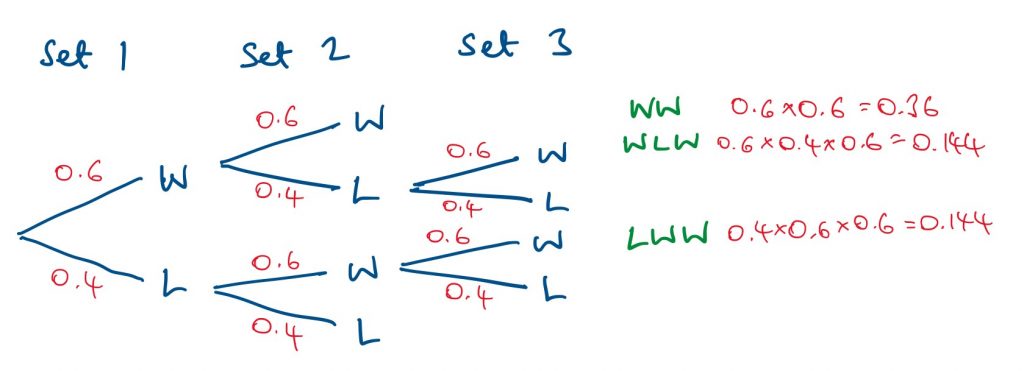
I started by assuming the stronger player would win each set with a probability of 0.6 and drew this tree diagram:
It looks a bit different from many tree diagrams, because there aren’t the same number of branches on every route through the diagram. If a player wins or loses the first two sets then the third set isn’t played.
At the right-hand side I have put the probabilities for the three routes where the stronger player wins. Adding these gives 0.648
This means that if p(wins one set) = 0.6, then p(wins a 3-set match) = 0.648
This fits with the early naïve thoughts: the probability the stronger player will win a 3-set match is higher than the probability they will win one set.
3-set match – a general tree diagram
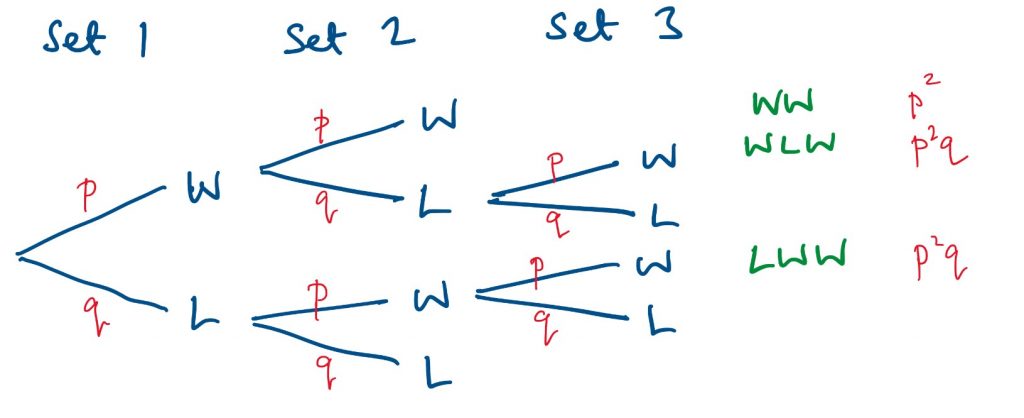
If I want to change the probability (say from 0.6 to 0.7) then I don’t want to have to draw a new diagram every time, so next I created a general diagram.
When working with probability we sometimes find it useful to break a usual algebraic convention. Normally we use as few letters as possible and if the probability that something occurs is x then the probability it doesn’t happen is (1 – x). This starts to get messy if we put lots of brackets on a tree diagram, so it is common to call the probability somethings happens p and the probability it doesn’t happen q (remembering, in case we need to use it later) that q = 1 – p.
Here is the general tree diagram.
The probability the stronger player wins is therefore p² + 2p²q
This table shows some values for p:
Unsurprisingly, when p = 0.5, the probability of winning the match is also 0.5
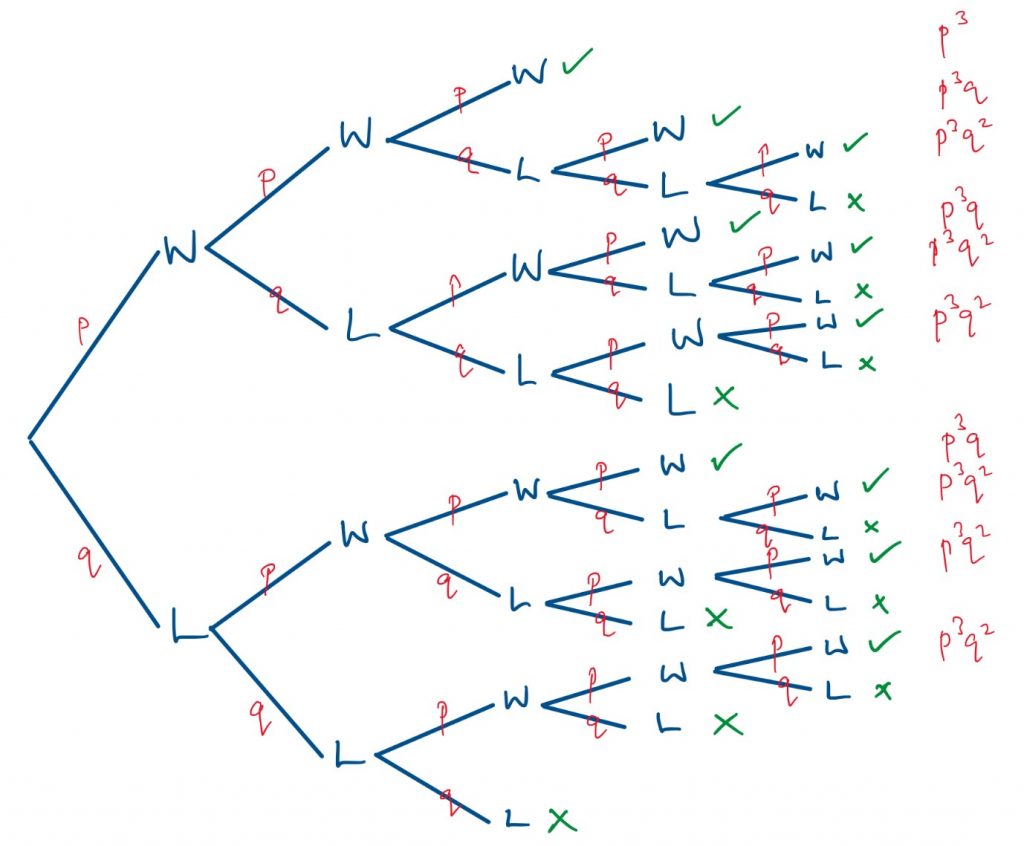
5-set match – a general tree diagram
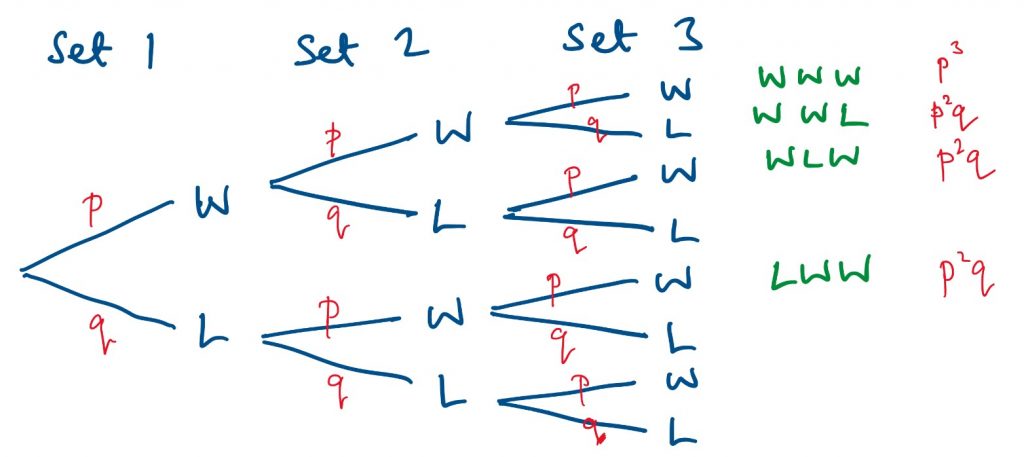
Here is the general tree diagram for a 5-set match.
This gives us P(wins match) = p³ + 3p³q + 6p³q²
The table is now updated with the 5-set figures. We can see that the probability of winning a 5-set match is higher (for the stronger player) than that of winning a 3-set match.
The values for p = 0.5 were not a surprise, but it was interesting that the disparity between 3-set and 5-set matches at p = 0.9 is smaller than when p = 0.7 or p = 0.8
I decided to draw a graph to show the two scenarios. I have changed p to x and have used (1 – x) in place of q. (This is drawn using Desmos, and the curly brackets to the right of the equations restrict the value of x to being between 0 and 1.)
This new formula helped me to realise some important things about the scenario. In p³ + 3p³q + 6p³q² I was initially surprised that every term had p³. That is (now) obvious: to win a 5-set match you have to win 3 sets.
I was also surprised to see that the coefficient of p³q was 3. There are 4 ways to arrange the letters p/p/p/q: pppq, ppqp, pqpp, qppp
So why is the coefficient 3 rather than 4? The first of these, pppq, wouldn’t ever crop up in a real match, because if a player wins the first 3 games then the match is over. And in fact, the eventual winner always wins the last set that is played!
Similarly, for the next term, we would ordinarily expect the coefficient of p³q² to be 10, but four of the arrangements end with a loss, so we need to ignore them.
This makes the algebra much more awkward, particularly if we want to consider what is happening with 7-set, or 9-set matches, etc (even though these don’t exist in real tournaments).
3-set match – the general tree diagram revisited
This version assumes that in every match all three sets are played, regardless of whether they would be in real life.
Our new equation is p³ + 3p²q. This looks rather different from p² + 2p²q, which we worked out earlier. Here’s the algebraic manipulation I carried out:
p³ + 3p²q
= p²(p + 3q)
= p²(p + q + 2q) but p + q equals 1
= p²(1 + 2q)
= p² + 2p²q which is what we had previously.
An alternative way to look at it is that the top branch (WW) has been replaced by WWW and WWL, which is the same thing, because the final set (which wouldn’t, in real life, be played) can only be won or lost, so those two probabilities add up to 1.
5-set match – towards a general formula
Because we are now going to pretend that all matches have 5 sets, we must have p at least 3 times, with the other 2 letters being either p or q.
We can have p 5 times. ppppp (which is p5) is the only way to do this.
Next we consider having p 4 times, with the other one being a q. We could start listing these (ppppq, pppqp, ppqpp, etc) but it is easy to see that q can appear in 5 different places so there are 5 different ways to arrange them. The simplified version of the algebra for each of these is p4, so we get 5p4.
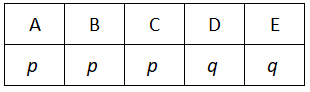
The last possibility is harder: we have p 3 times and q twice. We could make a list, but instead will consider the number of arrangements. If we have 5 distinct things (such as A, B, C, D and E) then there are 5 × 4 × 3 × 2 × 1 ways to arrange them. This is because there are 5 choices for the first position, then 4 remaining choices for the second position, 3 for the third, 2 for the fourth, and the final one that is left gives us no choice at all for the fifth one (which is why we multiply by 1). We often use the factorial notation 5! to stand for 5 × 4 × 3 × 2 × 1
There are therefore 120 ways to arrange the letters A, B, C, D and E. We can now map these onto the letters p and q like this:
D and E now both represent q, so if we change the order of DE we don’t get a new arrangement. For example, ABCDE and ABCED will be the same when D and E are both changed into q. This means we need to divide by 2.
We also need to consider that A, B and C are all p and are therefore indistinguishable. A, B and C can be arranged in 6 ways (this is 3! ), so we also need to divide by 6.
This gives us
![]() which is equal to 10. We need to add 10p3q2 to our expression.
which is equal to 10. We need to add 10p3q2 to our expression.
The full expression is therefore p5 + 5p4q + 10p3q2
This is the start of the binomial expansion of (p + q)5 and for this reason, probability where we have two possible outcomes is referred to as binomial probability.
What if we had a 7-set match?
It is now reasonably straightforward for us to move to other number of sets.
If we have a 7-set match we are interested in the situations where the stronger player wins at least 4 sets. This means we have p at least 4 times.
7 wins: p7
6 wins: 7p6q (the lost set could appear in any of the seven positions).
5 wins: we need p to appear 5 times, with q appearing twice. There are 7! ways to arrange 7 distinct things, but 5 of them are indistinguishable and so are the other 2, giving us
This gives us 21p5q2
4 wins: the coefficient is
The total probability the stronger player wins is therefore p7 + 7p6q + 21p5q2 + 35p4q3
Ever-increasing probability
I won’t show here my working out of the formula for 9-set, 11-set, etc, matches, but here is a table showing the probability that the stronger player wins a match if the probability they win any set is 0.6
How good is this model?
It is often useful to revisit our assumptions. This is what I decided at the start:
I am going to assign a probability that the stronger player wins each set and will assume that this is independent (ie that in a particular match the probability they will win a set is the same all the time).
I think that this is probably the most sensible way to model this problem, because it is reasonably straightforward in that it focuses only on the outcome of each set. Considering the outcome of each game would make this vastly more complicated, because the winner of a match that lasts 3 sets must win at least 18 games, and we would need to consider a different probability depending on whether the player is serving in a particular game or not.
I suspect that the probability a player wins a set does not remain constant throughout a match, because they may gain or lose confidence, injuries or tiredness may become an issue, etc. This means the probability a player wins set 2 is not independent of the probability they win set 1. Trying to deal with this would again make the model much more complicated.
Where next?
As an extension (for myself – at some point!) I want to reverse this process. I can look up the head-to-head results for two players and want to use those to work out the probability each one wins a single set. It will then be interesting to compare this to the number of sets that have been won/lost during their matches.
.
.