By Catriona Shearer (June 2020)
I recently discovered that typing ‘roll a dice’ into Google brings up a whole host of virtual dice to choose from. (‘Flip a coin’ and ‘spinner’ are also worth googling!)
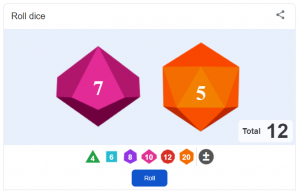
This discovery gave my colleague Ruth Colenso the idea of running a bingo game for the children of key workers we were supervising in school. The students created their own 4×4 grid of numbers, possibly including repeats, and we repeatedly rolled one 10-sided and one 20-sided dice on the interactive whiteboard. If the total was one of their numbers, they could cross it out.
This was only meant to be a 10-minute activity to give our group of Year 7s a break – they spend most of the day on their designated computers completing the same online learning as their peers. However, the competition was so engrossing that they convinced us to keep playing for an hour!
Ruth and I have both used a very similar idea before when teaching probability – often involving horse-racing animations, or Tarzan and Jane cartoons, but always using the total on two 6-sided dice. We were amazed at how long it took us to develop intuition when the dice weren’t identical (obviously, we couldn’t resist playing too and trying to beat the students!) and it certainly seemed to trip up our students too. When they picked numbers for their grids, they realised they couldn’t go over 30, but it was only mid-game that one realised she shouldn’t have picked 1 (we allowed her to change it!).
At the end of the game, with several students still waiting for 29 to appear, we talked about why it hadn’t been coming up as often as they expected, and started trying to list all the ways the totals 2, 3, 4, etc. could be made. The students were quick to spot that the bigger the number was, the more ways they could make it… but then why was filling the grid with 30s not a good idea? Maybe the ones in the middle were best: was 15 definitely the most likely number?
There’s a lot to explore here – I certainly won’t be limiting myself to two 6-sided dice in future!
In the next lesson, we went to repeat the same activity with a group of Year 8 and 9 students. They seemed to pick up the idea that ‘middling’ numbers were best much more intuitively, so we moved onto a more complicated proposal: the total from three dice, with 6, 10 and 12 sides.
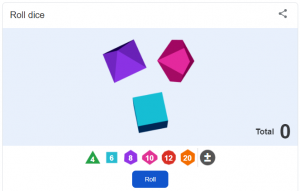
Now numbers from 3-28 were possible, but which were most likely? We played a game and found the winner had chosen mainly numbers in the teens and early twenties. Her strategy, though, had been to pick mainly even numbers because they had more factors than odd numbers. A useful reminder that students can sometimes seem to be completing a lesson very successfully, without really understanding the maths going on!
As a class, we decided to try and list all the ways of making particular totals from 3 dice. It quickly became clear that this was going to be a long-winded process! So we shared out the work between everyone in the room.
Even then, it was much more difficult than I’d anticipated. How do you ensure you’re being systematic, especially when some numbers have over 50 possible combinations? Here’s my method for counting 18 without writing everything out, which still took a whole page of working:
I found myself wishing I had a 3D spreadsheet to create a sample space diagram (six 10×12 grids would have worked, I suppose). Unfortunately, we ran out of time before we could categorically say which numbers are the most likely to be picked, so the problem remains unsolved. I’d like to try this again properly next time I teach probability, but perhaps I’ll limit myself to 4- and 6-sided dice to make the calculations a bit shorter.
Ruth and I are very proud of this new game (which we’re currently calling Multi-Dice Bingo until someone suggests a more exciting name) and will definitely use it again. After the lesson, we came up with a list of the features that recommend it over the versions we’ve used before:
- Students picked their own numbers, which gave them a degree of autonomy and made them much more invested in the game.
- The students can see each dice roll and don’t feel like they’re being tricked by the teacher (especially since they had free choice of numbers to pick).
- The first mathematical insights (don’t pick 1, and 2 or 30 aren’t great ideas either) came quickly, which meant students could see the value in analysing the game further.
- After these first insights, there was a lot to explore! More than we’d realised at the start.
- With rules like ‘first one to get a row, column or diagonal’, each game can be quick.
- Once students know the rules, it can be played again and again, for example, to fill a couple of minutes before the bell. This means students can improve their previous strategy with each iteration.
- There are countless variations (different sized dice, adding extra dice) which change the game in non-obvious ways. It never feels completely ‘solved’.
.
.
.