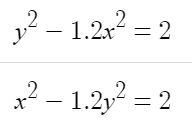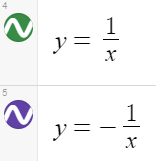(The creative possibilities of being bored.)
By Mark Dawes (March 2019)
I was recently on a course day away from school and during a coffee break I was bored. I had nothing to do and the others on my table were getting a cup of coffee, so I had no-one to talk to.
One of the pads of paper on the table was from a different organisation (nothing to do with the course I was on) and because I had nothing else to do I started thinking about the logo:
There are four nice curves there (presumably to refer to the four letters/subjects in ‘STEM’). I wondered what types of curve they could be. A cursory glance might suggest each one is a quadratic, but then it looks as if they could be asymptotic to the lines y = x and y = -x. Could this be two hyperbola graphs?
I have Desmos on my phone, so I could try it out and found these equations gave me the following graph. (All the screenshots here are taken from re-creations I made on the desktop version of Desmos.)
This looked promising!
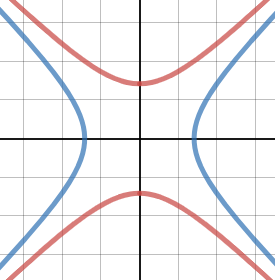
You can’t insert images into the Desmos phone app, so I used my laptop to add the logo to see whether it fitted well.
Close! Maybe it was not two hyperbolae, maybe the graphic designers started with this and made it look more artistically pleasing, or maybe I needed to tweak the equations slightly to stretch them.
A bit of trial and improvement led me to this:
And that gave the graph of:
I was happy that I had found the equations of the logo.
I put the pad down at an angle … and saw the logo anew like this:
Hold on: that looks rather like two reciprocal graphs!
Back to Desmos to find that these equations
give me this graph:
Is it plausible that a 45-degree rotation of a hyperbola would give a reciprocal graph? I hadn’t come across this before.
I returned to this over the subsequent few hours, worked out how to rotate graphs and to find the new equation and managed to convince myself. (This blogpost is too short to contain a full explanation and I wouldn’t want to spoil the fun for those who want to try it out for themselves!)
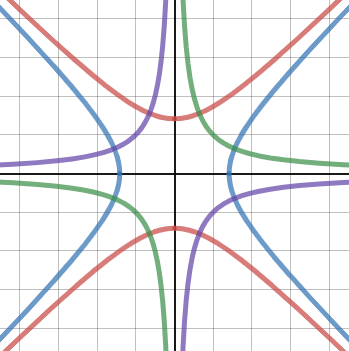
I will, however, leave you with one final screenshot from Desmos, of the hyperbolae and the reciprocals on the same graph:
Pretty, isn’t it!
So here was a situation where some initial boredom led me to think idly about a logo I had seen many times previously, and to think deeply about some curves, how to transform them and, in particular, how to rotate them.
The creative possibilities of boredom? Now that’s interesting!
.